1. Übersicht
Dieses Tutorial wurde für Tensorflow 2.2 aktualisiert.

In diesem Codelab lernen Sie, wie Sie ein neuronales Netzwerk erstellen und trainieren, das handschriftliche Ziffern erkennt. Während Sie Ihr neuronales Netzwerk optimieren, um eine Genauigkeit von 99% zu erreichen, lernen Sie auch die Tools kennen, mit denen Deep-Learning-Experten ihre Modelle effizient trainieren.
Dieses Codelab verwendet das MNIST-Dataset, eine Sammlung von 60.000 Ziffern mit Labels,die Generationen von PhDs fast zwei Jahrzehnte lang beschäftigt hat. Sie lösen das Problem mit weniger als 100 Zeilen Python-/TensorFlow-Code.
Lerninhalte
- Was ist ein neuronales Netzwerk und wie wird es trainiert?
- So erstellen Sie ein einfaches einschichtiges neuronales Netzwerk mit tf.keras
- So fügen Sie weitere Ebenen hinzu
- So richten Sie einen Lernratenzeitplan ein
- So erstellen Sie Convolutional Neural Networks
- Verwendung von Regularisierungstechniken: Dropout, Batchnormalisierung
- Was bedeutet Überanpassung?
Voraussetzungen
Nur ein Browser. Dieser Workshop kann vollständig mit Google Colaboratory durchgeführt werden.
Feedback
Bitte teilen Sie uns mit, wenn Ihnen in diesem Lab etwas fehlt oder Sie der Meinung sind, dass es verbessert werden sollte. Feedback wird über GitHub-Probleme [ feedback link] bearbeitet.
2. Kurzanleitung für Google Colaboratory
Für dieses Lab wird Google Colaboratory verwendet. Sie müssen nichts einrichten. Sie können es auf einem Chromebook ausführen. Öffnen Sie die Datei unten und führen Sie die Zellen aus, um sich mit Colab-Notebooks vertraut zu machen.
Zusätzliche Anweisungen findest du unten:
GPU-Back-End auswählen
Wählen Sie im Colab-Menü Laufzeit > Laufzeittyp ändern und dann „GPU“ auswählen. Die Verbindung zur Laufzeit erfolgt bei der ersten Ausführung automatisch. Alternativ können Sie „Verbinden“ verwenden oben rechts auf die Schaltfläche.
Notebook-Ausführung
Führen Sie einzelne Zellen aus, indem Sie auf eine Zelle klicken und die Umschalttaste und die Eingabetaste drücken. Sie können auch das gesamte Notebook ausführen. Wählen Sie dazu Laufzeit > Alle ausführen
Inhaltsverzeichnis
Alle Notebooks haben ein Inhaltsverzeichnis. Sie können ihn mit dem schwarzen Pfeil auf der linken Seite öffnen.
Ausgeblendete Zellen
Bei einigen Zellen wird nur der Titel angezeigt. Dies ist eine Colab-spezifische Notebook-Funktion. Sie können darauf doppelklicken, um den darin enthaltenen Code anzuzeigen, aber normalerweise ist er nicht sehr interessant. In der Regel Support- oder Visualisierungsfunktionen. Sie müssen diese Zellen trotzdem ausführen, damit die darin enthaltenen Funktionen definiert werden.
3. Neuronales Netzwerk trainieren
Zuerst sehen wir uns das Training eines neuronalen Netzwerks an. Öffnen Sie das Notebook unten und gehen Sie alle Zellen durch. Achten Sie noch nicht auf den Code, wir werden später damit beginnen.
Konzentrieren Sie sich beim Ausführen des Notebooks auf die Visualisierungen. Unten finden Sie eine entsprechende Erläuterung.
Trainingsdaten
Wir haben einen Datensatz mit handschriftlichen Ziffern, die beschriftet sind, damit wir wissen, was jedes Bild darstellt, d.h. eine Zahl zwischen 0 und 9. Im Notebook sehen Sie einen Auszug:

Das von uns erstellte neuronale Netzwerk klassifiziert die handschriftlichen Ziffern in ihren zehn Klassen (0, ..., 9). Dabei werden interne Parameter verwendet, die einen korrekten Wert haben müssen, damit die Klassifizierung funktioniert. Dieser „richtige Wert“ durch einen Trainingsprozess erlernt wird, der ein „Dataset mit Labels“ erfordert mit Bildern und den dazugehörigen richtigen Antworten.
Woher wissen wir, ob das trainierte neuronale Netzwerk gut funktioniert oder nicht? Das Trainings-Dataset zum Testen des Netzwerks zu verwenden, wäre Betrug. Das Dataset wurde bereits mehrmals während des Trainings erkannt und ist mit Sicherheit sehr leistungsfähig. Wir benötigen ein weiteres Dataset mit Labels, das während des Trainings noch nie gesehen wurde, um die „reale“ Leistung des Werbenetzwerks. Es wird als Validierungs-Dataset bezeichnet.
Training
Im Verlauf des Trainings werden die internen Modellparameter aktualisiert und das Modell erkennt immer besser die handschriftlichen Ziffern. Sie können ihn im Trainingsdiagramm sehen:
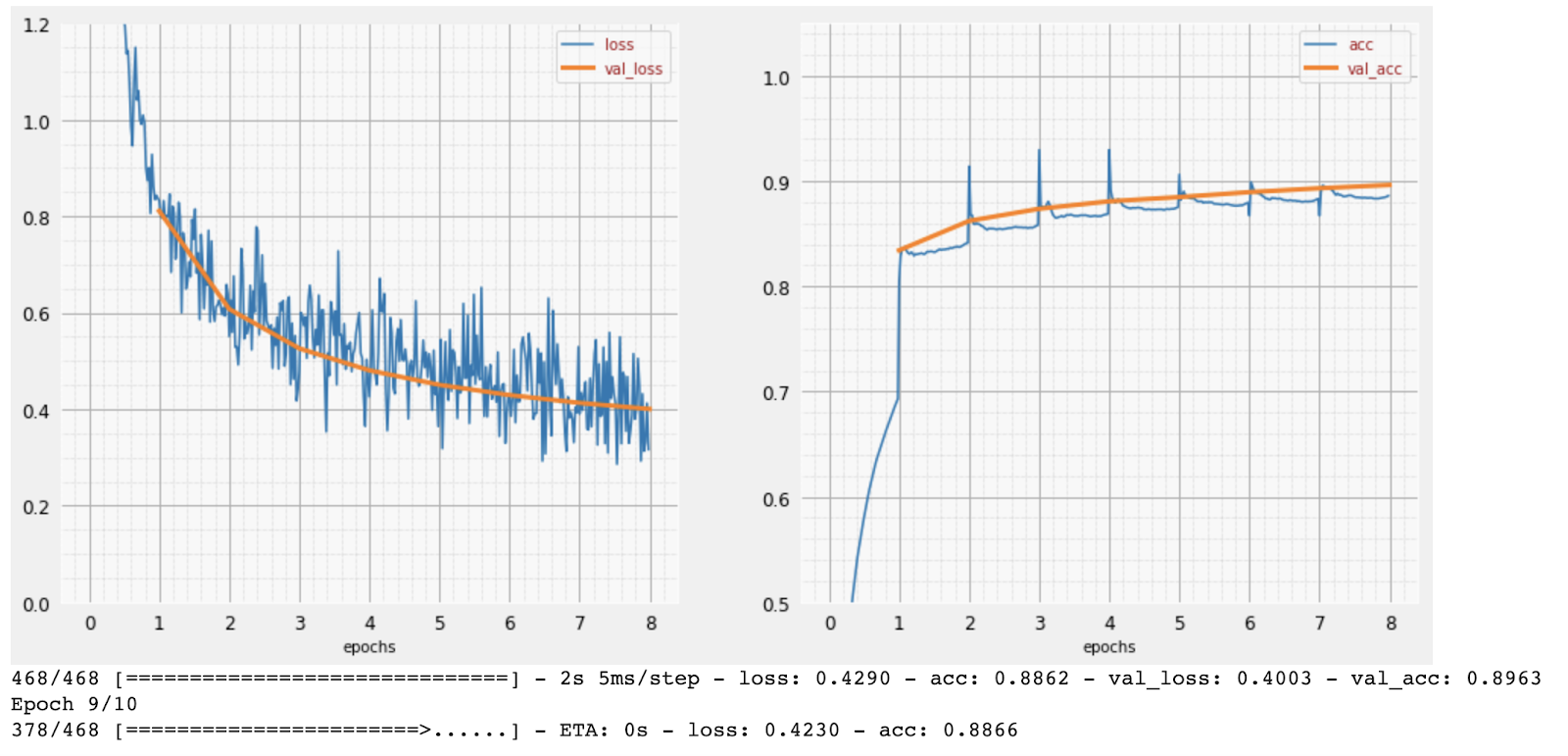
Die „Genauigkeit“ rechts ist einfach der Prozentsatz richtig erkannter Ziffern. Im Laufe des Trainings steigt er, was gut ist.
Links sehen wir den "loss" (Verlust). Um das Training voranzutreiben, definieren wir einen „Verlust“ , die angibt, wie schlecht das System die Ziffern erkennt und versucht, diese zu minimieren. Sie sehen hier, dass der Verlust sowohl bei den Trainings- als auch bei den Validierungsdaten im Laufe des Trainings sinkt. Das ist gut. Es bedeutet, dass das neuronale Netzwerk lernt.
Die X-Achse stellt die Anzahl der „Epochen“ dar. oder Iterationen über das gesamte Dataset.
Vorhersagen
Wenn das Modell trainiert wird, können wir damit handschriftliche Ziffern erkennen. Die nächste Visualisierung zeigt,wie gut sie bei einigen Ziffern aus lokalen Schriftarten (erste Zeile) und dann bei den 10.000 Ziffern des Validierungs-Datasets funktioniert. Die vorhergesagte Klasse wird unter jeder Ziffer in Rot angezeigt, wenn sie falsch war.

Wie Sie sehen, ist dieses erste Modell nicht sehr gut, erkennt aber noch einige Ziffern richtig. Die endgültige Validierungsgenauigkeit liegt bei etwa 90 %, was für das vereinfachte Modell, mit dem wir beginnen, nicht so schlecht ist, aber es bedeutet trotzdem, dass 1.000 von 10.000 Validierungsziffern fehlen. Das ist viel mehr, was angezeigt werden kann. Deshalb sieht es so aus, als wären alle Antworten falsch (rot).
Tensor
Daten werden in Matrizen gespeichert. Ein Graustufenbild mit 28 x 28 Pixel passt in eine zweidimensionale Matrix mit 28 x 28 Pixel. Für ein Farbbild brauchen wir jedoch mehr Abmessungen. Es gibt drei Farbwerte pro Pixel (Rot, Grün, Blau), sodass eine dreidimensionale Tabelle mit den Dimensionen [28, 28, 3] erforderlich ist. Zum Speichern eines Satzes von 128 Farbbildern ist eine vierdimensionale Tabelle mit den Abmessungen [128, 28, 28, 3] erforderlich.
Diese mehrdimensionalen Tabellen werden "Tensoren" genannt und die Liste ihrer Dimensionen ist ihre "Form".
4. [INFO]: Einführung in neuronale Netzwerke
Kurz und bündig
Wenn Ihnen alle im nächsten Absatz fett formatierten Begriffe bereits bekannt sind, können Sie mit der nächsten Übung fortfahren. Wenn Sie gerade erst mit dem Thema "Deep Learning" beginnen, ist dies willkommen. Bitte lesen Sie weiter.

Für Modelle, die als Folge von Ebenen erstellt wurden, bietet Keras die Sequential API an. Ein Bildklassifikator mit drei dichten Schichten kann beispielsweise in Keras so geschrieben werden:
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28, 1]),
tf.keras.layers.Dense(200, activation="relu"),
tf.keras.layers.Dense(60, activation="relu"),
tf.keras.layers.Dense(10, activation='softmax') # classifying into 10 classes
])
# this configures the training of the model. Keras calls it "compiling" the model.
model.compile(
optimizer='adam',
loss= 'categorical_crossentropy',
metrics=['accuracy']) # % of correct answers
# train the model
model.fit(dataset, ... )

Eine einzelne dichte Schicht
Handschriftliche Ziffern im MNIST-Dataset sind Graustufenbilder mit 28 × 28 Pixeln. Der einfachste Ansatz zur Klassifizierung besteht darin, 28 x 28=784 Pixel als Eingaben für ein neuronales einschichtiges Netzwerk zu verwenden.

Jedes „Neuron“ in einem neuronalen Netzwerk führt eine gewichtete Summe aller Eingaben durch und addiert eine Konstante, die als „Verzerrung“ bezeichnet wird. Anschließend wird das Ergebnis in eine nicht lineare Aktivierungsfunktion eingespeist. Die "weights" und "biases" sind Parameter, die durch Training bestimmt werden. Sie werden zuerst mit Zufallswerten initialisiert.
Das Bild oben zeigt ein einschichtiges neuronales Netzwerk mit 10 Ausgabeneuronalen, da wir Ziffern in 10 Klassen (0 bis 9) klassifizieren möchten.
Mit einer Matrixmultiplikation
So kann eine neuronale Netzwerkschicht, die eine Sammlung von Bildern verarbeitet, durch eine Matrixmultiplikation dargestellt werden:

Anhand der ersten Spalte mit Gewichtungen in der Gewichtungsmatrix W berechnen wir die gewichtete Summe aller Pixel des ersten Bildes. Diese Summe entspricht dem ersten Neuron. Mit der zweiten Spalte mit Gewichtungen machen wir dasselbe für das zweite Neuron und so weiter, bis das zehnte Neuron ist. Anschließend können wir den Vorgang für die restlichen 99 Bilder wiederholen. Wenn wir X die Matrix mit unseren 100 Bildern nennen, ergeben alle gewichteten Summen für unsere 10 Neuronen, berechnet aus 100 Bildern, einfach X.W, eine Matrixmultiplikation.
Jedes Neuron muss nun seine Verzerrung (eine Konstante) hinzufügen. Da wir zehn Neuronen haben, haben wir zehn Biaskonstanten. Wir nennen diesen Vektor von 10 Werten b. Dieser Wert muss jeder Zeile der zuvor berechneten Matrix hinzugefügt werden. Mit ein wenig Magie namens „Broadcasting“ schreiben wir dies mit einem einfachen Pluszeichen.
Schließlich wenden wir eine Aktivierungsfunktion an, zum Beispiel „Softmax“. (Erläuterung unten) und erhalten Sie die Formel, die ein neuronales Netz mit einer Schicht beschreibt, das auf 100 Bilder angewendet wird:

In Keras
Bei High-Level-Bibliotheken für neuronale Netzwerke wie Keras müssen wir diese Formel nicht implementieren. Es ist jedoch wichtig zu verstehen, dass eine neuronale Netzwerkschicht nur aus einer Reihe von Multiplikationen und Additionen besteht. In Keras würde eine dichte Ebene so geschrieben:
tf.keras.layers.Dense(10, activation='softmax')
Mehr Möglichkeiten
Es ist einfach, neuronale Netzwerkschichten zu verketten. In der ersten Ebene werden gewichtete Summen von Pixeln berechnet. Die nachfolgenden Ebenen berechnen gewichtete Summen der Ausgaben der vorherigen Ebenen.

Der einzige Unterschied, abgesehen von der Anzahl der Neuronen, ist die Wahl der Aktivierungsfunktion.
Aktivierungsfunktionen: Relu, Softmax und Sigmoid
In der Regel verwenden Sie Aktivierungsfunktion für alle bis auf die letzte Ebene. Die letzte Ebene in einem Klassifikator verwendet „Softmax“. Aktivierung.

Auch hier kann ein „Neuron“ berechnet eine gewichtete Summe aller Eingaben und addiert einen Wert namens „Verzerrung“ und übergibt das Ergebnis an die Aktivierungsfunktion.
Die gängigste Aktivierungsfunktion ist "RELU" für die gleichgerichtete Lineareinheit. Wie Sie in der Grafik oben sehen können, ist dies eine sehr einfache Funktion.
Die traditionelle Aktivierungsfunktion in neuronalen Netzwerken war das "Sigmoid", aber die "Relu" hat nachgewiesen, dass sie fast überall bessere Konvergenzeigenschaften aufweisen, und wird heute bevorzugt.

Softmax-Aktivierung für die Klassifizierung
Die letzte Schicht unseres neuronalen Netzwerks hat 10 Neuronen, weil wir handschriftliche Ziffern in 10 Klassen (0,...9) unterteilen möchten. Sie sollte 10 Zahlen zwischen 0 und 1 ausgeben, die die Wahrscheinlichkeit darstellen, dass diese Ziffer eine 0, eine 1, eine 2 usw. ist. Dazu verwenden wir auf dem letzten Layer die Aktivierungsfunktion "softmax".
Die Anwendung von Softmax auf einen Vektor erfolgt, indem die Exponentialfunktion jedes Elements ermittelt und dann der Vektor normalisiert wird, in der Regel durch Division des Werts durch „L1“. Norm (d.h. die Summe der absoluten Werte), sodass normalisierte Werte addiert 1 ergeben und als Wahrscheinlichkeiten interpretiert werden können.
Das Ergebnis der letzten Schicht vor der Aktivierung wird manchmal als "logits" bezeichnet. Wenn dieser Vektor L = [L0, L1, L2, L3, L4, L5, L6, L7, L8, L9] ist, dann:


Kreuzentropieverlust
Nachdem nun unser neuronales Netzwerk Vorhersagen aus Eingabebildern produziert, müssen wir messen, wie gut sie sind, d.h. den Abstand zwischen dem, was uns das Netzwerk mitteilt, und den richtigen Antworten, die oft als „Labels“ bezeichnet werden. Denken Sie daran, dass wir die korrekten Labels für alle Bilder im Dataset haben.
Jede Entfernung würde funktionieren, aber für Klassifizierungsprobleme wäre die sogenannte „Kreuzentropie-Distanz“. ist am effektivsten. Wir bezeichnen dies als Fehler oder „Verlust“. :

Gradientenabstieg
„Schulung“ Das neuronale Netzwerk bedeutet, Trainingsbilder und -labels zu verwenden, um Gewichtungen und Verzerrungen so anzupassen, dass die Kreuzentropie-Verlustfunktion minimiert wird. Und so funktioniert es:
Die Kreuzentropie ist eine Funktion von Gewichtungen, Verzerrungen, Pixeln des Trainingsbilds und seiner bekannten Klasse.
Wenn wir die partiellen Ableitungen der Kreuzentropie relativ zu allen Gewichtungen und allen Verzerrungen berechnen, erhalten wir einen "Gradienten", der für ein bestimmtes Bild, Label und den Gegenwartswert von Gewichtungen und Verzerrungen berechnet wird. Denken Sie daran, dass wir Millionen von Gewichtungen und Verzerrungen haben können, sodass die Berechnung des Farbverlaufs wie eine Menge Arbeit klingt. Zum Glück erledigt TensorFlow das für uns. Die mathematische Eigenschaft eines Farbverlaufs besteht darin, dass er nach oben zeigt. Da wir hingehen möchten, wo die Kreuzentropie gering ist, gehen wir in die entgegengesetzte Richtung. Gewichtungen und Verzerrungen werden um einen Bruchteil des Farbverlaufs aktualisiert. Dann wiederholen wir das und verwenden die nächsten Batches von Trainingsbildern und ‐labels in einer Trainingsschleife. Hoffentlich nähert sich dies einem Punkt an, an dem die Kreuzentropie minimal ist, obwohl nichts garantiert, dass dieses Minimum einzigartig ist.

Mini-Batching und Dynamik
Sie können Ihren Gradienten nur für ein Beispielbild berechnen und die Gewichtungen und Gewichtungen sofort aktualisieren. Bei einem Batch von beispielsweise 128 Bildern ergibt sich jedoch ein Farbverlauf, der die Einschränkungen durch verschiedene Beispielbilder besser darstellt und daher wahrscheinlich schneller der Lösung näherkommt. Die Größe des Mini-Batches ist ein anpassbarer Parameter.
Diese Technik, die manchmal auch als „stochastisches Gradientenabstieg“ bezeichnet wird hat einen weiteren, pragmatischeren Vorteil: Die Arbeit mit Batches bedeutet auch, mit größeren Matrizen zu arbeiten, und diese lassen sich in der Regel einfacher für GPUs und TPUs optimieren.
Die Konvergenz kann jedoch immer noch etwas chaotisch sein und sogar aufhören, wenn der Gradientenvektor nur Nullen enthält. Bedeutet das, dass wir ein Minimum gefunden haben? Nimmt immer. Eine Farbverlaufskomponente kann bei einem Mindest- oder Höchstwert null sein. Bei einem Gradientenvektor mit Millionen von Elementen ist die Wahrscheinlichkeit, dass jede Null einem Minimum und keines von ihnen einem Höchstpunkt entspricht, ziemlich gering, wenn alle Nullen sind. In einem Raum mit vielen Dimensionen kommen Sattelpunkte häufig vor, sodass wir nicht bei ihnen anhalten möchten.

Illustration: ein Sattelpunkt. Der Farbverlauf ist 0, aber kein Mindestwert in alle Richtungen. (Bildzuordnung Wikimedia: By Nicoguaro – Own work, CC BY 3.0)
Die Lösung besteht darin, dem Optimierungsalgorithmus etwas Schwung zu verleihen, damit er die Sattelpunkte überwinden kann, ohne anzuhalten.
Glossar
batch oder mini-batch: Das Training wird immer mit Batches von Trainingsdaten und Labels durchgeführt. So kann der Algorithmus konvergieren. Der „Batch“ Dimension ist in der Regel die erste Dimension von Datentensoren. Zum Beispiel enthält ein Tensor mit der Form [100, 192, 192, 3] 100 Bilder mit 192 × 192 Pixeln mit drei Werten pro Pixel (RGB).
Kreuzentropieverlust: eine spezielle Verlustfunktion, die häufig in Klassifikatoren verwendet wird.
dichte Schicht: Eine Schicht aus Neuronen, bei der jedes Neuron mit allen Neuronen aus der vorherigen Schicht verbunden ist.
features: Die Eingaben eines neuronalen Netzwerks werden manchmal als „Features“ bezeichnet. Die Kunst, herauszufinden, welche Teile eines Datasets (oder Kombinationen von Teilen) in ein neuronales Netzwerk eingespeist werden sollen, um gute Vorhersagen zu erhalten, wird als „Feature Engineering“ bezeichnet.
labels: ein anderer Name für "Klassen" oder richtige Antworten bei einem beaufsichtigten Klassifizierungsproblem
Lernrate: Anteil des Gradienten, um den Gewichtungen und Verzerrungen bei jeder Iteration der Trainingsschleife aktualisiert werden.
Logits: Die Ausgaben einer Neuronenschicht vor Anwendung der Aktivierungsfunktion werden als "Logits" bezeichnet. Der Begriff leitet sich von der „logistischen Funktion“ ab, auch bekannt als die „Sigmoidfunktion“ Dies war früher die am häufigsten verwendete Aktivierungsfunktion. „Neuron gibt vor logistische Funktion aus“ als „logits“ abgekürzt.
loss: die Fehlerfunktion, die die Ausgaben neuronaler Netzwerke mit den richtigen Antworten vergleicht
neuron: berechnet die gewichtete Summe der Eingaben, fügt eine Verzerrung hinzu und speist das Ergebnis über eine Aktivierungsfunktion ein.
One-Hot-Codierung: Klasse 3 von 5 wird als Vektor aus 5 Elementen codiert, alle Nullen mit Ausnahme des dritten, also 1.
relu: korrigierte lineare Einheit. Eine beliebte Aktivierungsfunktion für Neuronen.
Sigmoid: Eine weitere Aktivierungsfunktion, die früher häufig verwendet wurde und in Sonderfällen immer noch nützlich ist.
Softmax-Parameter: eine spezielle Aktivierungsfunktion, die auf einen Vektor wirkt, die Differenz zwischen der größten und allen anderen Komponenten erhöht und außerdem den Vektor auf die Summe 1 normalisiert, sodass er als Vektor von Wahrscheinlichkeiten interpretiert werden kann. Wird als letzter Schritt in Klassifikatoren verwendet.
tensor: Ein "Tensor" ist wie eine Matrix, aber mit einer beliebigen Anzahl von Dimensionen. Ein eindimensionaler Tensor ist ein Vektor. Ein zweidimensionaler Tensor ist eine Matrix. Dann können Sie Tensoren mit 3, 4, 5 oder mehr Dimensionen haben.
5. Sehen wir uns den Code an.
Kehren wir zum Studiennotizbuch zurück und lesen wir diesmal den Code.
Gehen wir alle Zellen in diesem Notebook durch.
Zelle „Parameter“
Hier werden die Batchgröße, die Anzahl der Trainingsphasen und der Speicherort der Datendateien definiert. Datendateien werden in einem Google Cloud Storage-Bucket (GCS) gehostet. Deshalb beginnt ihre Adresse mit gs://.
Zelle „Importe“
Alle erforderlichen Python-Bibliotheken werden hier importiert, einschließlich TensorFlow und matplotlib für Visualisierungen.
Zelle „visualization utilities [RUN ME]****“
Diese Zelle enthält uninteressanten Visualisierungscode. Die Ansicht ist standardmäßig minimiert, aber Sie können sie öffnen und sich den Code ansehen, wenn Sie Zeit haben, indem Sie darauf doppelklicken.
Zelle "tf.data.Dataset: Dateien parsen und Trainings- und Validierungs-Datasets vorbereiten"
In dieser Zelle wurde die tf.data.Dataset API verwendet, um das MNIST-Dataset aus den Datendateien zu laden. Sie müssen nicht zu viel Zeit mit dieser Zelle verbringen. Wenn Sie sich für die tf.data.Dataset API interessieren, finden Sie in diesem Tutorial zu Datenpipelines mit TPU-Geschwindigkeit. Zunächst sind die Grundlagen:
Bilder und Labels (richtige Antworten) aus dem MNIST-Dataset werden in 4 Dateien in Datensätzen mit fester Länge gespeichert. Die Dateien können mit der dedizierten Aufzeichnungsfunktion geladen werden:
imagedataset = tf.data.FixedLengthRecordDataset(image_filename, 28*28, header_bytes=16)
Wir haben jetzt ein Dataset mit Bildbyte. Sie müssen in Bilder decodiert werden. Dafür definieren wir eine Funktion. Das Bild ist nicht komprimiert, sodass die Funktion nichts decodieren muss (decode_raw führt praktisch nichts aus). Das Bild wird dann in Gleitkommawerte zwischen 0 und 1 konvertiert. Wir könnten es hier in ein 2D-Bild umformen, aber eigentlich behalten wir es als ein flaches Array mit Pixeln der Größe 28*28, da unsere anfängliche dichte Schicht dies erwartet.
def read_image(tf_bytestring):
image = tf.io.decode_raw(tf_bytestring, tf.uint8)
image = tf.cast(image, tf.float32)/256.0
image = tf.reshape(image, [28*28])
return image
Wir wenden diese Funktion mithilfe von .map auf das Dataset an und rufen ein Dataset mit Bildern ab:
imagedataset = imagedataset.map(read_image, num_parallel_calls=16)
Auf die gleiche Art werden Labels gelesen und decodiert. Dabei .zip verwenden wir Bilder und Labels zusammen:
dataset = tf.data.Dataset.zip((imagedataset, labelsdataset))
Wir haben jetzt ein Dataset mit Paaren (Bild, Label). Das erwartet unser Modell. Wir sind noch nicht ganz bereit, sie in der Trainingsfunktion zu verwenden:
dataset = dataset.cache()
dataset = dataset.shuffle(5000, reshuffle_each_iteration=True)
dataset = dataset.repeat()
dataset = dataset.batch(batch_size)
dataset = dataset.prefetch(tf.data.experimental.AUTOTUNE)
Die tf.data.Dataset API verfügt über alle erforderlichen Dienstprogrammfunktionen zum Vorbereiten von Datasets:
.cache speichert das Dataset im RAM. Da dies ein winziges Dataset ist, funktioniert es. .shuffle ordnet die Datei mit einem Puffer von 5.000 Elementen nach dem Zufallsprinzip an. Es ist wichtig, dass Trainingsdaten gut zufällig angeordnet werden. .repeat führt eine Schleife des Datasets aus. Daran werden wir mehrmals (über mehrere Epochen) trainieren. .batch führt mehrere Bilder und Labels zu einem Mini-Batch zusammen. Schließlich kann .prefetch die CPU verwenden, um den nächsten Batch vorzubereiten, während der aktuelle Batch auf der GPU trainiert wird.
Das Validierungs-Dataset wird auf ähnliche Weise vorbereitet. Jetzt können wir ein Modell definieren und mit diesem Dataset trainieren.
Zelle „Keras Model“
Alle unsere Modelle sind gerade Abfolgen von Ebenen, sodass wir sie mit dem Stil tf.keras.Sequential erstellen können. Anfangs ist es hier eine einzelne dichte Schicht. Sie hat zehn Neuronen, weil wir handschriftliche Ziffern in zehn Klassen unterteilen. Es wird „Softmax“ verwendet. da dies die letzte Ebene in einem Klassifikator ist.
Ein Keras-Modell muss außerdem die Form seiner Eingaben kennen. tf.keras.layers.Input kann verwendet werden, um sie zu definieren. Hier sind Eingabevektoren flache Vektoren von Pixelwerten der Länge 28 × 28.
model = tf.keras.Sequential(
[
tf.keras.layers.Input(shape=(28*28,)),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='sgd',
loss='categorical_crossentropy',
metrics=['accuracy'])
# print model layers
model.summary()
# utility callback that displays training curves
plot_training = PlotTraining(sample_rate=10, zoom=1)
Die Konfiguration des Modells erfolgt in Keras mithilfe der Funktion model.compile. Hier verwenden wir die Basisoptimierung 'sgd' (Stochastic Gradient Descent). Ein Klassifizierungsmodell erfordert eine Kreuzentropie-Verlustfunktion, die in Keras als 'categorical_crossentropy' bezeichnet wird. Schließlich bitten wir das Modell, den Messwert 'accuracy' zu berechnen, also den Prozentsatz richtig klassifizierter Bilder.
Keras bietet das sehr schöne Dienstprogramm model.summary(), das die Details des von Ihnen erstellten Modells ausgibt. Die Lehrkraft hat das Dienstprogramm PlotTraining hinzugefügt (in der Zelle „visualization utilities“ definiert), mit dem während des Trainings verschiedene Trainingskurven angezeigt werden.
Zelle „Modell trainieren und validieren“
Hier wird das Training durchgeführt, indem model.fit aufgerufen und die Trainings- und Validierungs-Datasets übergeben werden. Standardmäßig führt Keras am Ende jeder Epoche eine Validierung durch.
model.fit(training_dataset, steps_per_epoch=steps_per_epoch, epochs=EPOCHS,
validation_data=validation_dataset, validation_steps=1,
callbacks=[plot_training])
In Keras ist es möglich, während des Trainings mithilfe von Callbacks benutzerdefinierte Verhaltensweisen hinzuzufügen. So wurde das sich dynamisch aktualisierende Trainingsdiagramm für diesen Workshop implementiert.
Zelle „Vorhersagen visualisieren“
Sobald das Modell trainiert ist, können wir Vorhersagen abrufen, indem wir model.predict() aufrufen:
probabilities = model.predict(font_digits, steps=1)
predicted_labels = np.argmax(probabilities, axis=1)
Hier haben wir zu Testzwecken eine Reihe von gedruckten Ziffern vorbereitet, die aus lokalen Schriftarten gerendert werden. Denken Sie daran, dass das neuronale Netzwerk einen Vektor mit zehn Wahrscheinlichkeiten aus seinem endgültigen „Softmax“ zurückgibt. Um das Label zu erhalten, müssen wir herausfinden, welche Wahrscheinlichkeit die höchste ist. Hierfür benötigen Sie np.argmax aus der NumPy-Bibliothek.
Um zu verstehen, warum der axis=1-Parameter erforderlich ist, denken Sie daran, dass wir einen Batch von 128 Bildern verarbeitet haben und das Modell daher 128 Wahrscheinlichkeitsvektoren zurückgibt. Die Form des Ausgabetensors ist [128, 10]. Wir berechnen den argmax-Wert über die 10 Wahrscheinlichkeiten, die für jedes Bild zurückgegeben werden, also axis=1 (die erste Achse ist 0).
Dieses einfache Modell erkennt bereits 90% der Ziffern. Nicht schlecht, aber Sie werden dies jetzt erheblich verbessern.

6. Ebenen hinzufügen

Um die Erkennungsgenauigkeit zu verbessern, fügen wir dem neuronalen Netzwerk weitere Ebenen hinzu.

Wir behalten „Softmax“ als Aktivierungsfunktion auf der letzten Ebene bei, da dies für die Klassifizierung am besten funktioniert. Bei Zwischenschichten verwenden wir jedoch die klassische Aktivierungsfunktion: das Sigmoid:

Ihr Modell könnte beispielsweise so aussehen (vergessen Sie die Kommas nicht, tf.keras.Sequential verwendet eine durch Kommas getrennte Liste von Ebenen):
model = tf.keras.Sequential(
[
tf.keras.layers.Input(shape=(28*28,)),
tf.keras.layers.Dense(200, activation='sigmoid'),
tf.keras.layers.Dense(60, activation='sigmoid'),
tf.keras.layers.Dense(10, activation='softmax')
])
Sehen Sie sich die Zusammenfassung an. Ihres Modells nutzen. Sie hat jetzt mindestens zehnmal mehr Parameter. Das sollte 10-mal besser sein. Aber aus irgendeinem Grund ...

Die Niederlage scheint auch über das Dach geschossen worden zu sein. Irgendetwas stimmt nicht.
7. Besondere Pflege bei tiefen Netzwerken
Sie haben gerade neuronale Netzwerke kennengelernt, wie sie in den 80er und 90er Jahren entwickelt wurden. Kein Wunder, dass sie diese Idee aufgegeben haben und damit den sogenannten „KI-Winter“ einläuten. Je mehr Ebenen hinzugefügt werden, desto schwieriger wird das Konvergieren neuronaler Netzwerke.
Es hat sich herausgestellt, dass neuronale Deep-Learning-Netzwerke mit vielen Schichten (20, 50 und heute sogar 100) sehr gut funktionieren können, wenn sie einige mathematische Tricks für die Konvergierung der Daten enthalten. Die Entdeckung dieser einfachen Tricks ist einer der Gründe für die Renaissance des Deep Learnings in den 2010er Jahren.
RELU-Aktivierung

Die Sigmoid-Aktivierungsfunktion ist in tiefen Netzwerken eigentlich ziemlich problematisch. Sie drückt alle Werte zwischen 0 und 1 zusammen. Wenn Sie dies wiederholt tun, können die Ausgaben von Neuronen und deren Gradienten vollständig verschwinden. Es wurde aus historischen Gründen erwähnt, aber moderne Netzwerke verwenden die RELU (Rektifizierte lineare Einheit), die so aussieht:

Die Relu hingegen hat eine Ableitung von 1, zumindest auf der rechten Seite. Dank der RELU-Aktivierung gibt es immer noch andere, die einen klaren Farbverlauf ungleich null haben, selbst wenn die Gradienten einiger Neuronen null sein können, und das Training kann in einem guten Tempo fortgesetzt werden.
Ein besseres Optimierungstool
In sehr hochdimensionalen Bereichen wie hier – wir haben eine Größenordnung von 10.000 Gewichtungen und Verzerrungen – „Sattelpunkte“ häufig auftreten. Dies sind Punkte, die kein lokales Minima sind, aber an denen der Farbverlauf immer noch null ist und das Optimierungstool für das Gradientenabstieg dort bleibt. TensorFlow verfügt über eine breite Palette von Optimierungstools, darunter einige, die mit einem gewissen Trägheitsgrad arbeiten und sicher über Sattelpunkte hinwegsegeln.
Zufällige Initialisierungen
Die Kunst der Initialisierung von Gewichtsverzerrungen vor dem Training ist selbst ein Forschungsbereich, zu dem zahlreiche Artikel veröffentlicht werden. Eine Übersicht über alle in Keras verfügbaren Initialisierer finden Sie hier. Glücklicherweise verhält sich Keras standardmäßig richtig und verwendet den Initialisierer 'glorot_uniform', der in fast allen Fällen die beste Lösung ist.
Sie müssen nichts weiter tun, denn Keras tut bereits das Richtige.
NaN ???
Die Kreuzentropieformel beinhaltet einen Logarithmus und log(0) ist keine Zahl (NaN, gegebenenfalls ein numerischer Absturz). Kann die Eingabe für die Kreuzentropie 0 sein? Die Eingabe stammt aus Softmax, die im Wesentlichen eine exponentielle und eine Exponentialfunktion ist, die nie null ist. Wir sind also in Sicherheit!
Wirklich? In der schönen Welt der Mathematik wären wir sicher, aber in der Computerwelt ist exp(-150), dargestellt im float32-Format, so NULL wie nur möglich und die Kreuzentropie stürzt ab.
Glücklicherweise brauchen Sie auch hier nichts zu tun, da Keras dies übernimmt und Softmax-Werte gefolgt von der Kreuzentropie besonders sorgfältig berechnet, um numerische Stabilität zu gewährleisten und die gefürchteten NaNs zu vermeiden.
Erfolg?

Sie sollten jetzt eine Genauigkeit von 97% erreichen. Das Ziel in diesem Workshop ist ein deutlich über 99 %, also machen wir weiter.
Wenn Sie nicht weiterkommen, finden Sie hier die Lösung:
8. Abnahme der Lernrate
Vielleicht können wir versuchen, schneller zu trainieren? Die Standardlernrate im Adam-Optimierungstool ist 0,001. Versuchen wir, es zu erhöhen.
Schneller zu sein scheint nicht viel zu helfen, und was ist das für ein Geräusch?

Die Trainingskurven sind sehr laut und es werden beide Validierungskurven betrachtet: Sie springen nach oben und unten. Das bedeutet, dass wir zu schnell arbeiten. Wir könnten zur vorherigen Geschwindigkeit zurückkehren, aber es gibt einen besseren Weg.

Die gute Lösung besteht darin, schnell zu starten und die Lernrate exponentiell zu verringern. In Keras können Sie dies mit dem tf.keras.callbacks.LearningRateScheduler-Callback tun.
Nützlicher Code zum Kopieren und Einfügen:
# lr decay function
def lr_decay(epoch):
return 0.01 * math.pow(0.6, epoch)
# lr schedule callback
lr_decay_callback = tf.keras.callbacks.LearningRateScheduler(lr_decay, verbose=True)
# important to see what you are doing
plot_learning_rate(lr_decay, EPOCHS)
Vergessen Sie nicht, die von Ihnen erstellte lr_decay_callback zu verwenden. Füge ihn der Liste der Callbacks in model.fit hinzu:
model.fit(..., callbacks=[plot_training, lr_decay_callback])
Die Auswirkungen dieser kleinen Änderung sind spektakulär. Sie sehen, dass das Rauschen größtenteils verschwindet und die Testgenauigkeit nun beständig über 98% liegt.

9. Absturz, Überanpassung
Das Modell scheint jetzt gut zu koordinieren. Versuchen wir, noch tiefer in das Thema einzutauchen.
Hilft es?

Nicht wirklich, die Genauigkeit bleibt immer noch bei 98 %, und wir sehen uns den Validierungsverlust an. Es geht nach oben! Der Lernalgorithmus arbeitet nur mit Trainingsdaten und optimiert den Trainingsverlust entsprechend. Validierungsdaten werden nie erkannt. Daher überrascht es nicht, dass sich seine Arbeit nach einiger Zeit nicht mehr auf den Validierungsverlust auswirkt, der nicht mehr abfällt und manchmal sogar wieder zurückfällt.
Dies wirkt sich nicht unmittelbar auf die realen Erkennungsfähigkeiten Ihres Modells aus, hindert Sie jedoch daran, viele Iterationen auszuführen, und ist in der Regel ein Zeichen dafür, dass das Training keine positiven Auswirkungen mehr hat.

Diese Trennung wird normalerweise als „Überanpassung“ bezeichnet. Dann können Sie versuchen, eine Regularisierungstechnik namens „Dropout“ anzuwenden. Die Dropout-Technik schießt bei jedem Trainingsdurchlauf zufällige Neuronen.
Hat es funktioniert?

Das Rauschen tritt wieder auf (nicht überraschend, wie das Dropout funktioniert). Der Validierungsverlust scheint nicht mehr zu werden, ist aber insgesamt höher als ohne Dropout. Und die Validierungsgenauigkeit ist etwas gesunken. Das ist ziemlich enttäuschend.
Offenbar war das Dropout nicht die richtige Lösung oder vielleicht „Überanpassung“. ist ein komplexeres Konzept und einige der Ursachen lassen sich nicht für ein "Dropout" einsetzen. beheben?
Was ist „Überanpassung“? Zu einer Überanpassung kommt es, wenn ein neuronales Netzwerk „schlecht“ lernt, und zwar in einer Weise, die für die Trainingsbeispiele funktioniert, aber nicht so gut mit realen Daten. Es gibt Regularisierungstechniken wie Dropouts, die ein besseres Lernen zwingen können, aber eine Überanpassung hat auch tiefere Wurzeln.

Zu einer einfachen Überanpassung kommt es, wenn ein neuronales Netzwerk zu viele Freiheitsgrade für das vorliegende Problem hat. Stellen Sie sich vor, wir haben so viele Neuronen, dass das Netzwerk alle unsere Trainingsbilder darin speichern und dann durch einen Musterabgleich erkennen kann. Bei realen Daten würde es vollständig scheitern. Ein neuronales Netzwerk muss etwas eingeschränkt sein, damit es erzwungen wird, das Gelernte während des Trainings zu generalisieren.
Wenn Sie nur sehr wenige Trainingsdaten haben, kann selbst ein kleines Netzwerk sie auswendig lernen und Sie werden eine „Überanpassung“ feststellen. Im Allgemeinen benötigen Sie zum Trainieren neuronaler Netzwerke immer viele Daten.
Wenn Sie alles im Buch erledigt haben, mit verschiedenen Netzwerkgrößen experimentieren, um sicherzustellen, dass seine Freiheitsgrade beschränkt werden, Aussetzer angewandt und mit vielen Daten trainiert wurden, stecken Sie möglicherweise immer noch auf einem Leistungsniveau, das nicht verbessert werden könnte. Das bedeutet, dass Ihr neuronales Netzwerk in seiner jetzigen Form nicht in der Lage ist, weitere Informationen aus Ihren Daten zu extrahieren, wie in unserem Fall hier.
Erinnern Sie sich noch daran, wie wir unsere Bilder verwenden, die in einem einzigen Vektor zusammengefasst sind? Das war eine wirklich schlechte Idee. Handschriftliche Ziffern bestehen aus Formen. Beim Abflachen der Pixel haben wir die Forminformationen verworfen. Es gibt jedoch eine Art neuronales Netz, das Forminformationen nutzen kann: Convolutional Networks. Probieren wir sie aus.
Wenn Sie nicht weiterkommen, finden Sie hier die Lösung:
10. [INFO] Convolutional Networks
Kurz und bündig
Wenn Ihnen alle im nächsten Absatz fett formatierten Begriffe bereits bekannt sind, können Sie mit der nächsten Übung fortfahren. Wenn Sie gerade erst mit Convolutional Neural Networks anfangen, lesen Sie bitte weiter.

Illustration: Bildfilterung mit zwei aufeinanderfolgenden Filtern aus jeweils 4 × 3=48 lernbaren Gewichten.
So sieht ein einfaches Convolutional Neural Network in Keras aus:
model = tf.keras.Sequential([
tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(kernel_size=3, filters=12, activation='relu'),
tf.keras.layers.Conv2D(kernel_size=6, filters=24, strides=2, activation='relu'),
tf.keras.layers.Conv2D(kernel_size=6, filters=32, strides=2, activation='relu'),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(10, activation='softmax')
])

In einer Schicht eines Convolutional Network, ein "Neuron" eine gewichtete Summe der direkt darüber liegenden Pixel, nur über einen kleinen Bereich des Bildes hinweg. Sie fügt eine Verzerrung hinzu und füttert die Summe durch eine Aktivierungsfunktion, so wie es ein Neuron in einer regulären dichten Schicht tun würde. Dieser Vorgang wird dann für das gesamte Bild mit denselben Gewichtungen wiederholt. Denken Sie daran, dass in dichten Schichten jedes Neuron eine eigene Gewichtung hatte. Hier wird ein einzelnes "Patch" von Gewichtungen gleitet in beide Richtungen über das Bild (eine "Faltung"). Die Ausgabe hat so viele Werte, wie Pixel im Bild enthalten sind. An den Rändern ist jedoch ein gewisser Abstand erforderlich. Es handelt sich um einen Filtervorgang. In der obigen Abbildung wird ein Filter von 4x4x3=48 Gewichtungen verwendet.
48 Gewichtungen reichen jedoch nicht aus. Um weitere Freiheitsgrade hinzuzufügen, wiederholen wir denselben Vorgang mit einem neuen Satz von Gewichtungen. Dies erzeugt einen neuen Satz von Filterausgaben. Nennen wir es einen „Kanal“, der Ausgabewerte analog zu den R-, G- und B-Kanälen im Eingabebild.

Die zwei (oder mehr) Gewichtungssätze können durch Hinzufügen einer neuen Dimension zu einem Tensor addiert werden. Damit erhalten wir die generische Form des Tensors für die Gewichtung für eine Faltungsschicht. Da die Anzahl der Eingabe- und Ausgabekanäle Parameter sind, können wir mit dem Stapeln und Verketten von Faltungsschichten beginnen.

Illustration: Ein Convolutional Neural Network transformiert „Cubes“ von Daten in andere „Cubs“ von Daten.
Schrittweise Faltungen, max. Pooling
Wenn wir die Faltungen mit einer Schrittzahl von 2 oder 3 ausführen, können wir den resultierenden Datenwürfel auch in seiner horizontalen Dimension verkleinern. Hierfür gibt es zwei gängige Methoden:
- Gestrichelte Faltung: ein gleitender Filter wie oben, aber mit einer Schrittlänge > 1
- Max. Pooling: ein gleitendes Fenster, in dem der MAX-Vorgang angewendet wird (in der Regel auf 2 x 2 Patches, wiederholt alle 2 Pixel)

Illustration: Das Verschieben des Rechenfensters um 3 Pixel führt zu weniger Ausgabewerten. Gestrichelte Faltungen oder Max-Pooling (Maximum auf einem 2 x 2-Fenster, das in einem Schritt von 2 verschoben wird) sind eine Möglichkeit, den Datenwürfel in horizontalen Dimensionen zu verkleinern.
Die letzte Ebene
Nach der letzten Faltungsschicht haben die Daten die Form eines Würfels. Es gibt zwei Möglichkeiten, sie in die endgültige dichte Schicht zu speisen.
Die erste besteht darin, den Datenwürfel in einem Vektor zu vereinfachen und ihn dann in die Softmax-Ebene zu übergeben. Manchmal können Sie sogar eine dichte Ebene vor der Softmax-Ebene einfügen. Dies ist in der Regel teuer, was die Anzahl der Gewichtungen angeht. Eine dichte Schicht am Ende eines Faltungsnetzwerks kann mehr als die Hälfte der Gewichte des gesamten neuronalen Netzwerks haben.
Anstatt eine teure dichte Schicht zu verwenden, können wir den „Cube“ der eingehenden Daten in so viele Teile wie Klassen unterteilen, den Durchschnitt der Werte ermitteln und diese über eine Softmax-Aktivierungsfunktion einspeisen. Diese Art der Erstellung des Klassifizierungskopfs kostet 0 Gewichtungen. In Keras gibt es eine Ebene dafür: tf.keras.layers.GlobalAveragePooling2D().

Im nächsten Abschnitt können Sie ein Faltungsnetzwerk für das vorliegende Problem erstellen.
11. Ein Convolutional Network
Lassen Sie uns ein Faltungsnetzwerk für die Erkennung handschriftlicher Ziffern aufbauen. Wir verwenden oben drei Convolutional Layers, unten unsere traditionelle Softmax-Readout-Ebene, und verbinden sie mit einer vollständig verbundenen Ebene:

Beachten Sie, dass die zweite und dritte Faltungsebene eine Schrittzahl von zwei haben, was erklärt, warum sie die Anzahl der Ausgabewerte von 28x28 auf 14x14 und dann auf 7x7 reduzieren.
Schreiben wir nun den Keras-Code.
Vor der ersten Convolutional Layer ist besondere Aufmerksamkeit erforderlich. Tatsächlich wird ein Würfel in 3D erwartet. aber unser Dataset wurde bisher für dichte Schichten eingerichtet und alle Pixel der Bilder werden zu einem Vektor vereinfacht. Wir müssen sie wieder in 28x28x1-Bilder (1 Kanal für Graustufenbilder) umwandeln:
tf.keras.layers.Reshape(input_shape=(28*28,), target_shape=(28, 28, 1))
Sie können diese Linie anstelle der bisher verwendeten tf.keras.layers.Input-Ebene verwenden.
In Keras lautet die Syntax für eine „Relu“-aktivierte Convolutional Layer:

tf.keras.layers.Conv2D(kernel_size=3, filters=12, padding='same', activation='relu')
Für eine gestaffelte Faltung würden Sie Folgendes schreiben:
tf.keras.layers.Conv2D(kernel_size=6, filters=24, padding='same', activation='relu', strides=2)
So vereinfachen Sie einen Datenwürfel zu einem Vektor, damit er von einer dichten Ebene verwendet werden kann:
tf.keras.layers.Flatten()
Und für die dichte Schicht hat sich die Syntax nicht geändert:
tf.keras.layers.Dense(200, activation='relu')
Hat Ihr Modell die Genauigkeitsgrenze von 99% überschritten? Ganz nah dran... aber schauen wir uns die Validierungsverlustkurve an. Kommt Ihnen das bekannt vor?

Sieh dir auch die Vorhersagen an. Erstmals sollten Sie sehen, dass die meisten 10.000 Testziffern jetzt korrekt erkannt werden. Es sind nur noch etwa 41⁄2 Zeilen falsch erkannter Fehler übrig (etwa 110 von 10.000 Ziffern)

Wenn Sie nicht weiterkommen, finden Sie hier die Lösung:
12. Erneuter Abbruch
Das vorherige Training weist deutliche Anzeichen für eine Überanpassung auf (und liegt immer noch unter einer Genauigkeit von 99 %). Sollen wir es noch einmal versuchen?
Wie lief es diesmal?

Offenbar hat das Dropout dieses Mal funktioniert. Der Validierungsverlust nimmt nicht mehr zu und die endgültige Genauigkeit sollte deutlich über 99 % liegen. Glückwunsch!
Als wir das erste Mal versucht haben, Dropout anzuwenden, dachten wir, wir hätten ein Überanpassungsproblem, obwohl das Problem tatsächlich in der Architektur des neuronalen Netzwerks lag. Ohne Convolutional Layer wären wir nicht weiter gekommen und das Dropout könnte nichts tun.
Dieses Mal scheint es, als ob eine Überanpassung die Ursache des Problems war, und das Dropout hat tatsächlich geholfen. Denken Sie daran, dass es viele Faktoren gibt, die zu einer Abweichung zwischen der Trainings- und der Validierungsverlustkurve führen können, sodass der Validierungsverlust schleichend wächst. Eine Überanpassung (zu viele Freiheitsgrade, wird vom Netzwerk schlecht genutzt) ist nur eine davon. Wenn Ihr Dataset zu klein ist oder die Architektur Ihres neuronalen Netzwerks nicht ausreicht, beobachten Sie möglicherweise ein ähnliches Verhalten bei den Verlustkurven, aber ein Dropout wird nicht helfen.
13. Batchnormalisierung
Schließlich versuchen wir, eine Batchnormalisierung hinzuzufügen.
Das ist die Theorie. Denken Sie in der Praxis an ein paar Regeln:
Lassen Sie uns fürs Erste eine Batch-Norm-Ebene auf jeder neuronalen Netzwerkschicht außer der letzten hinzufügen. Nicht zum letzten Softmax-Parameter hinzufügen Ebene. Es wäre dort nicht hilfreich.
# Modify each layer: remove the activation from the layer itself.
# Set use_bias=False since batch norm will play the role of biases.
tf.keras.layers.Conv2D(..., use_bias=False),
# Batch norm goes between the layer and its activation.
# The scale factor can be turned off for Relu activation.
tf.keras.layers.BatchNormalization(scale=False, center=True),
# Finish with the activation.
tf.keras.layers.Activation('relu'),
Wie ist die Genauigkeit jetzt?

Mit etwas Feinabstimmung (BATCH_SIZE=64, Lernrate-Abfallparameter 0.666, Abbruchrate auf der dichten Ebene 0.3) und etwas Glück können Sie 99, 5 % erreichen. Die Anpassung der Lernrate und der Abbruchrate erfolgte gemäß den Best Practices zur Verwendung der Batchnorm:
- Die Batchnormalisierung erleichtert das Konvergieren neuronaler Netzwerke und ermöglicht in der Regel ein schnelleres Training.
- Die Batch-Norm ist ein Regularizer. In der Regel können Sie die Anzahl der Dropouts verringern oder sogar überhaupt nicht verwenden.
Das Lösungs-Notebook hat eine Trainingsausführung von 99,5 %:
14. In der Cloud auf leistungsstarker Hardware trainieren: AI Platform

Im Ordner „mlengine“ auf GitHub finden Sie eine für die Cloud geeignete Version des Codes mit einer Anleitung zur Ausführung auf der Google Cloud AI Platform. Bevor Sie diesen Teil ausführen können, müssen Sie ein Google Cloud-Konto erstellen und die Abrechnung aktivieren. Die für das Lab erforderlichen Ressourcen sollten unter ein paar Dollar liegen (bei einer Trainingszeit von 1 Stunde für eine GPU). So bereiten Sie Ihr Konto vor:
- Erstellen Sie ein Google Cloud Platform-Projekt ( http://cloud.google.com/console).
- Aktivieren Sie die Abrechnung.
- Installieren Sie die GCP-Befehlszeilentools ( GCP SDK hier).
- Erstellen Sie einen Google Cloud Storage-Bucket (in der Region
us-central1). Er wird verwendet, um den Trainingscode bereitzustellen und das trainierte Modell zu speichern. - Aktivieren Sie die erforderlichen APIs und fordern Sie die erforderlichen Kontingente an. Wenn Sie den Trainingsbefehl einmal ausführen, sollten Sie Fehlermeldungen erhalten, die Ihnen mitteilen, was Sie aktivieren müssen.
15. Glückwunsch!
Sie haben Ihr erstes neuronales Netzwerk gebaut und bis zu einer Genauigkeit von 99% trainiert. Die dabei erlernten Techniken sind nicht spezifisch für das MNIST-Dataset, sondern werden häufig bei der Arbeit mit neuronalen Netzwerken eingesetzt. Als Abschiedsgeschenk hier sind die „Notizen der Klippen“ für das Labor in Cartoon-Version. Sie können sich damit merken, was Sie gelernt haben:

Weiteres Vorgehen
- Nach vollständig verbundenen und Convolutional Networks sollten Sie sich recurrent Neural Networks ansehen.
- Zum Ausführen von Trainings oder Inferenzen in der Cloud auf einer verteilten Infrastruktur bietet Google Cloud die AI Platform.
- Zu guter Letzt freuen wir uns über Feedback. Bitte teilen Sie uns mit, wenn Ihnen in diesem Lab etwas fehlt oder Sie der Meinung sind, dass es verbessert werden sollte. Feedback wird über GitHub-Probleme [ feedback link] bearbeitet.

|
|
Copyright für alle Cartoonbilder in diesem Lab: alexpokusay / 123RF Stockfotos


 Der Autor: Martin GörnerTwitter:
Der Autor: Martin GörnerTwitter: 